Due vecchi compagni di liceo decidono di incontrarsi dopo tanto tempo, dopo aver scoperto, grazie a un social network, di trovarsi nella stessa città. Uno di loro si è laureato in matematica e ora insegna in università il corso di "teoria dei modelli"; l'altro è uno scapestrato artista che si guadagna da vivere girando l'Europa con la sua arte.
ARTISTA: Quindi insegni in università adesso? Chi l'avrebbe mai detto? Non io di certo: credevo che le tue propensioni fossero altre. Quale corso sei riuscito a guadagnarti?
MATEMATICO: In realtà non era nei miei piani né nelle mie aspettative, ma poi ho saputo di una cattedra vacante in un corso di laurea magistrale sulla teoria dei modelli. Non potevo perdere l'occasione.
ARTISTA: "Teoria dei modelli"? Wow!
MATEMATICO: Non mi aspettavo che tu capissi...
ARTISTA: In effetti non so di cosa parli: per me i "modelli" sono le persone che uso come soggetti dei miei quadri, delle mie opere.
MATEMATICO: Direi proprio che ci occupiamo di cose diverse. Due mondi diversi.
ARTISTA: Ah no, aspetta! Un modello è anche uno schizzo, un bozzetto, quello che si segue e si perfeziona per la stesura dell'opera finale. Sai quanti modelli ha dovuto creare Canova prima di realizzare il capolavoro "Amore e Psiche"? E' una parte fondamentale del processo creativo. Insomma... devo supporre che ti sia dato all'arte anche tu?
MATEMATICO: Ma no! Il modello è una costruzione prettamente teorica, capisci? La tua è un'interpretazione estremamente superficiale.
ARTISTA: Disapprovo, ma voglio proprio conoscere il tuo pensiero a riguardo. Illuminami.
MATEMATICO: Non pretenderei mai di spiegarti di cosa mi occupo, né tantomeno cosa sia un modello nella logica matematica. O cosa sia a logica matematica. Ma nel caso più semplice e generico, nelle scienze, il modello è una rappresentazione quantitativa, mentale, una mera schematizzazione che si presta per spiegare un fenomeno nella maniera più fedele possibile: avrai almeno sentito parlare di modello matematico di un sistema fisico, chimico, biologico, e via dicendo. Ma non è realtà, non è materia, spesso non è neanche perfetto. E' uno strumento.
ARTISTA: E poi voi matematici negate di essere i re dell'astrazione? Vivete nel mondo delle idee! Ad ogni modo, ti assicuro che il modello ha vita propria al di fuori dell'ideale e della scienza. Se proprio non vuoi fidarti del tuo scapestrato amico artista, fidati dell'industria, dell'ingegneria! Ti direi anche della moda, ma perderei presto la tua attenzione, per cui passerò oltre. Non sei forse arrivato qui con il tuo nuovo modello di FIAT? E secondo te le catene di produzione su cosa si basano? Su progetti, su modelli in scala, sulla loro realizzazione e sulla loro riproducibilità. E per l'arte non è molto diverso, come ho già tentato di spiegarti. Amico mio, il modello è pura realtà, sussiste in questa, è concretizzazione di un'idea, non l'idea stessa. Quello fuori del mondo, almeno per una volta, mi sembri tu.
MATEMATICO: Sai, potresti quasi avermi smosso, fosse anche di un solo millimetro, dalla mia idea. Potrei proporti un compromesso: una frase di un matematico e scienziato che ho ammirato moltissimo e che tuttora è esempio - e modello, per rimanere in tema - per me. Marvin Minsky in un articolo scrisse: "A è modello della realtà B per un osservatore C, se l'osservatore C ponendo domande ad A ottiene risposte relative a B".
ARTISTA: Non vorrei sbagliare, ma non mi sembra che questo contraddica in alcun modo la mia visione: la realtà "B" può essere, per esempio, un ritratto; "A" sarebbe la modella che posa per me, "C" sei tu che, conoscendo a priori l'opera, guardando la modella, ne riconosci la rappresentazione. Ti disturba questa interpretazione?
MATEMATICO: A dire il vero no, credo che tu abbia colto nel segno, e credo che Minsky abbia creato una definizione che può essere realmente universale, che escluderebbe a prescindere il motivo stesso della nostra discussione. Avrei dovuto nominarlo prima!
ARTISTA: Già, avresti dovuto! Finalmente un matematico che scende dall'iperuranio, oserei quasi dire "pragmatico": questa sì che è bella!... Bada bene, mi riferisco a lui, non a te.
MATEMATICO: Non hai perso la voglia di scherzare, vedo, in tutti questi anni.
ARTISTA: Mai! Ma ora, possiamo finalmente ordinare i nostri caffè?
Visualizzazione post con etichetta matematica. Mostra tutti i post
Visualizzazione post con etichetta matematica. Mostra tutti i post
venerdì 5 giugno 2020
martedì 26 maggio 2020
Da non perdere...
"Quando, dopo le rivoluzioni della scienza e dell’industria, la scienza si impadronisce dello strumento lagrangiano delle Fonctions Analytiques, gli scienziati, che ancora si chiamano philosophes, hanno la certezza di poter descrivere con le funzioni matematiche l’universo dei fenomeni. Uno strumento matematico capace di gestire i fenomeni dinamici, variabili nel tempo, ponendo in relazione gli effetti con le cause che li hanno prodotti, dimostra almeno sulla carta le sue enormi potenzialità. [...]
Possiamo considerare lo stato attuale dell'universo come l'effetto del suo passato e la causa del suo futuro. Un intelletto che ad un determinato istante dovesse conoscere tutte le forze che mettono in moto la natura, e tutte le posizioni di tutti gli oggetti di cui la natura è composta, se questo intelletto fosse inoltre sufficientemente ampio da sottoporre questi dati ad analisi, esso racchiuderebbe in un'unica formula i movimenti dei corpi più grandi dell'universo e quelli degli atomi più piccoli; per un tale intelletto nulla sarebbe incerto ed il futuro proprio come il passato sarebbe evidente davanti ai suoi occhi.
[...] Prima della rivoluzione scientifica il criterio di similitudine fondato epistemologicamente sui teoremi di Euclide ammetteva la conoscenza del mondo in una dimensione lineare e riproducibile. I canoni della perfezione dell'uomo vitruviano, alla base delle stesse regole costruttive dell’architettura (non solo edile, ma dell’intero universo) erano stati minati dallo stesso Galilei con le sue considerazioni sulla non-linearità della natura, e avevano trovato nella metafora dell’osso del gigante la loro forma più immediata di una comunicazione destinata anche ai non scienziati.
D’ora in poi, anche se ancora priva delle macchine da calcolo, la scienza procederà per modelli: strutture logiche fondate sugli algoritmi, supportate dalla semantica dei segni e organizzate in gerarchie tassonomiche.
Ma l’ approccio quantitativo definitivo arriverà molto più tardi solo quando la rivoluzione elettronica renderà risolvibili numericamente problemi sino ad allora insoluti e farà nascere la moderna teoria dei sistemi e dei modelli. [...]"
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Crediti: Blog "Philosophy and engineering" del professor Vittorio Marchis, "Ingegnerie della divinazione (5) - L'illusione del determinismo"
martedì 19 maggio 2020
giovedì 14 maggio 2020
STEP #16 - Marvin Minsky "testimonial" del modello
specializzato nel campo dell'intelligenza artificiale (IA). Fu cofondatore dell'Artificial Intelligence Project presso il MIT e autore di numerosi testi riguardanti l'IA e la filosofia.
Spesso egli ritornò sul concetto di "modello" come "paradigma", non solo nell'ambito matematico ma nella più assoluta generalità. E' da attribuire a lui una delle più chiare e complete definizioni moderne del termine, che ci spinge a sceglierlo come "testimonial" per eccellenza:
"A è modello della realtà B per un osservatore C, se l'osservatore C ponendo domande ad A ottiene risposte relative a B"
Tale citazione appartiene ad un articolo da lui scritto intitolato "Matter, Minds and Models",
in cui egli tenta di spiegare la relazione tra eventi fisici e mentali e il ruolo fondamentale che la creazione di un modello può rivestire.
"If a creature can answer a question about a hypothetical experiment without actually performing it, then it has demonstrated some knowledge about the world. For, his answer to the question must be an encoded description of the behavior (inside the creature) of some sub-machine or "model" responding to an encoded description of the world situation described by the question [...]"
E' merito del modello, afferma dunque Minsky, se una creatura può rispondere ad una domanda su un ipotetico esperimento senza realizzarlo realmente: esso, infatti, conferisce una sorta di descrizione decodificata di una determinata situazione nel mondo.
Per leggere l'articolo completo:
martedì 21 aprile 2020
La teoria dei modelli
La teoria dei modelli è una branca della matematica, e più precisamente della logica, che affronta lo studio generalizzato del concetto di modello, in riferimento alle relazioni tra varie strutture ed in particolare alla soddisfacibilità di date teorie.
venerdì 17 aprile 2020
Frase del giorno
"Mathematics can not be applied to reality without an intermediate model."
-N. Cartwright - How the laws of physics lie Oxford New York (1983)
-N. Cartwright - How the laws of physics lie Oxford New York (1983)
mercoledì 25 marzo 2020
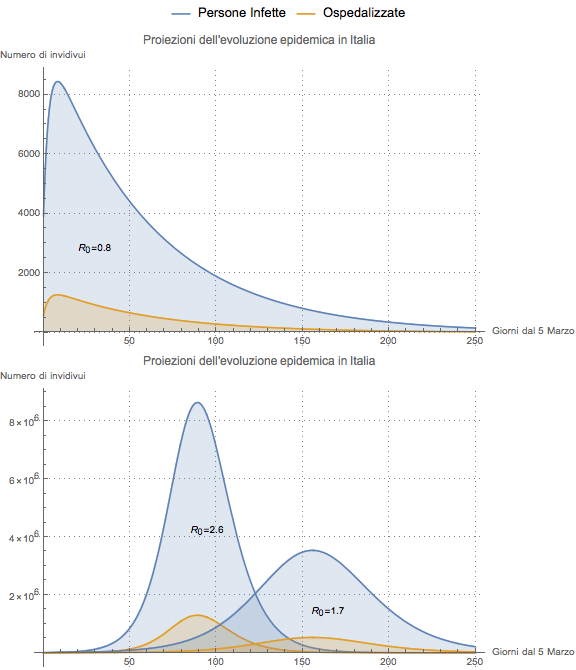
Attualità: Coronavirus e modello SIR
Le scienze, in generale, si servono della modellizzazione matematica dei concetti, fondamentale per garantire analisi accurate dei fenomeni. Non fanno eccezione, ovviamente, le scienze biologiche, tra queste la branca dell'epidemiologia, attualmente sotto i riflettori vista la recente espansione del virus Covid-19 a livello mondiale.
Di seguito riporto il link di un'accurata definizione del cosiddetto modello SIR, esempio di modellizzazione dinamica delle malattie infettive, e un grafico esemplificativo:
martedì 24 marzo 2020
Iscriviti a:
Post (Atom)